一、引入
先举一个小栗子。
一数组有 $n$ 个元素,有 $m$ 次询问($n, m <= 10^5$)。对于每次询问给出 $l, r$,求出 $[l, r]$的区间和。
有的同学说,这很简单啊!直接前缀和不就行了吗?确实如此,示例代码如下:
int n, m; cin >> n >> m;
vector< int > sum( n + 10 );
fill( sum.begin(), sum.end(), 0 );
for ( int i = 1, x; i <= n; ++i ) {
cin >> x;
sum[ i ] = sum[ i - 1 ] + x;
}
while ( m-- ) {
int l, r; cin >> l >> r;
l = min( l, r ); r = max( l, r );
cout << sum[ r ] - sum[ l - 1 ] << endl;
}
但是,我们稍稍改变一下题目,将求区间和改为求区间最大值,前缀和就行不通了。我们应该如何在 $O(nlogn)$ 的时间复杂度下求得结果呢?
二、ST 算法介绍
上面的问题也被称为区间最值查询。($RMQ$, $Range $ $Maximum/Minimum$ $Query$)在静态的区间最值查询问题中,我们可以使用 $ST$ 算法解决。
首先我们假定需要求解的数组为 $A={ 10, 20, 30, 40, 50, 60 }$,且为了方便,数组下标从 $ 1 $ 开始。
由于问题可离线,我们可以先预处理,再输出答案。
基于倍增思想,我们可以对于每一个元素构造一个倍增数组,其内容为$A$ 中 $[i, i+2^k-1]$的最大值($i\in( [1,n]\cap\N), i+2^k-1\leq n, k\in \N$),如下图所示:
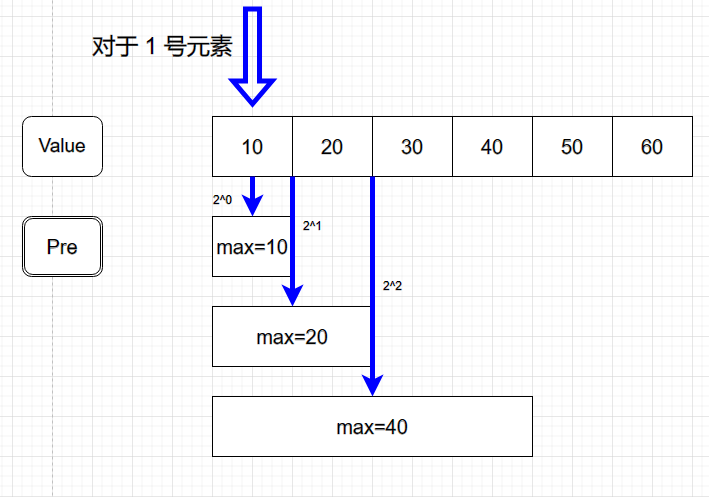
以此类推,我们可以对于每个元素构造这么一个数组,即 $Pre$ 数组为一个二维数组,可定义为:
int pre[ maxn ][ maxlog ]; // maxlog 为上文中 k 的最大值,一般取 25 左右
那么,我们该如何快速求解出 $pre[i][j]$ 呢?
三、 pre[i][j] 的求法
我们可以将 $ST$ 算法看作一个 DP。
首先,$pre[i][j]$ 本身就可以视作一个状态矩阵,存储着对应区间的最值。
接着,其边界条件是 $pre[i][0]$,即元素本身。这很容易理解,因为 $[i,i]$ 的最值本身就是 $i$ 嘛。
其次,由于预处理是离线过程,所以对于新的区间最值求解,不会对已求出区间的最值产生影响,故满足 DP 的无后效性原则。
最后,我们来整理状态转移方程。
对于区间 $[i, j]$,显然可以将其二分为 $[i, \frac{i+j}{2}]$ 和 $(\frac{i+j}{2},j)$。若知道这两个区间的最值 $p$ 和 $q$,显然地,整个$[i,j]$区间的最值必然等于$max(p,q)$或$min(p,q)$。这样问题就转化为求子区间的最值。以此类推直至边界。我们可以结合下图进行理解。
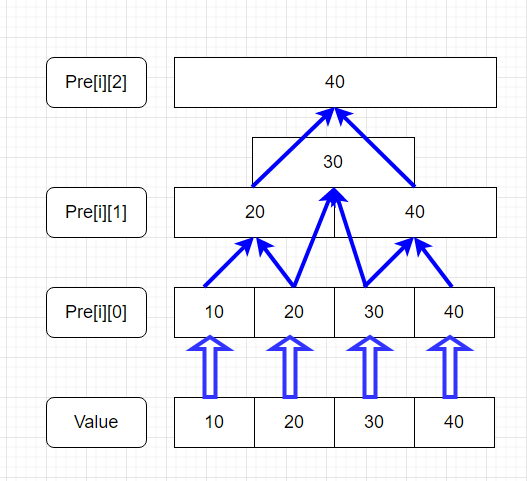
于是我们可以轻松写出代码:
int n, m; cin >> n >> m;
for ( int i = 1; i <= n; ++i ) cin >> pre[ i ][ 0 ];
for ( int j = 1; j <= maxlog; ++j )
for ( int i = 1; i + ( 1 << j ) - 1 <= n; ++i )
pre[ i ][ j ] = max(
pre[ i ][ j - 1 ], // [i, i+2^(j-1)-1] 即前半段区间
pre[ i + ( 1 << ( j - 1 ) ) ][ j - 1 ] // [i+2^(j-1), i+2^j-1] 即后半段区间
); // 因为 2^j = 2 * 2^(j-1),所以可以这么写
四、How to query?
预处理完毕,该如何实现高效查询呢?
要求的区间为 $[l, r]$,区间长度即为 $r-l+1$。得知了区间长度,我们就可以在 $Pre$ 中进行查找。由于区间长度不一定为 $ 2^k, k\in N $,我们仅取一个区间返回结果不一定准确(因为 $Pre$ 中预处理的区间长度均为 $ 2^k $)所以我们需要找到一个长度,使得其为 $ 2^k $ 且尽量长但不超过 $[l,r]$ 的长度。显然地,这个长度为 $floor(\log_{2}{(r-l+1)})$。这个长度可以直接用于 $Pre$ 且尽量大。所以所取区间为 $[l, l+2^{log_{2}{(r-l+1)}}-1]$,在 $Pre$ 数组中即为 $ pre[l][log(r-l+1)]$。 对于 $\complement_{[l, l+2^{log_{2}{(r-l+1)}}-1]}{[l,r]}$,由于 $RMQ$ 问题的可重复贡献性,我们可以找两段重叠的区间取最值。所以可以从 $r$ 开始向左找长度同样为 $floor(\log_{2}{(r-l+1)})$ 的区间,使这个区间右端点为 $r$。于是第二个区间为 $ [r-2^{log_{2}{(r-l+1)}}+1,r] $,对应 $Pre$ 中即为 $pre[r-(1<<log(r-l+1))+1][log(r-l+1)]$ 。不难发现这两个区间的并集必为 $[l,r]$。即两个区间最值的 $max/min$ 一定是整个区间的最值。通过图片进行解释:
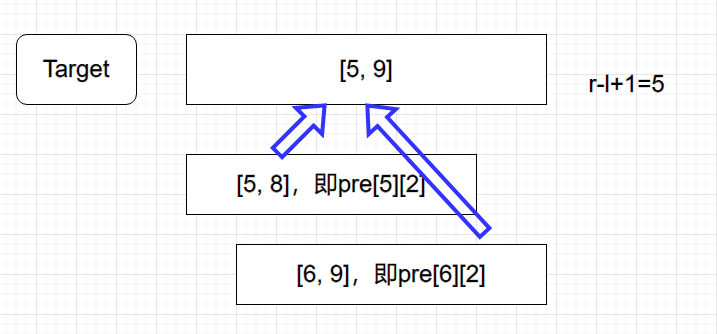
于是我们可得出 $query$ 函数的代码:
inline int query( int l, int r ) {
int k = log( r - l + 1 ); // 简化代码
return max(
pre[ l ][ k ],
pre[ r - ( 1 << k ) + 1 ][ k ]
);
}
下面是 $ST$ 算法的模板。用于解决洛谷 P3865:
#include <bits/stdc++.h>
using namespace std;
#define k lg2[r - l + 1]
typedef long long ll;
template<typename T>
inline void read(T &x) {
T f = 1; x = T(0); char ch = getchar();
while (!isdigit(ch)) { if (ch == '-') f = -1; ch = getchar(); }
while (isdigit(ch)) { x = x * 10 + ch - '0'; ch = getchar(); }
x *= f;
}
namespace SparseTable {
const int MAXN = 2e6 + 10, MAXLOG = 25;
int n, m, f[MAXN][MAXLOG], lg2[MAXN];
void init(void) {
// Read components
read(n); read(m);
for (int i = 1; i <= n; i++)
read(f[i][0]);
// Sparse Table
for (int j = 1; j <= MAXLOG; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++)
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1) )][ j - 1 ]);
// Log2
lg2[1] = 0; lg2[2] = 1;
for (int i = 3; i < MAXN; i++)
lg2[i] = lg2[i / 2] + 1;
}
inline int query(const int l, const int r) {
return max(f[l][k], f[r - (1 << k) + 1][k]);
}
}
int main(void) {
int l, r;
SparseTable::init();
while ( (SparseTable::m) --) {
read(l); read(r);
printf("%d\n", SparseTable::query(min(l, r), max(l, r)));
}
return 0;
}
六、优点与局限性
$ST$ 算法有一些其他算法所不具备的优点,比如:
- 代码量小
- 常数小,时间复杂度较低
$ST$ 算法的局限性很大,只能解决静态区间可重复贡献问题,局限性如下:
- 可扩展性较弱
- 无法处理在线修改操作
第二点实际上是 $ST$ 表实际应用中最大的障碍。那么,如何解决在线修改查询问题呢?需要的两大杀器分别是树状数组和线段树(包括 zkw 线段树),这两种数据结构将在接下来的几篇文章中介绍。
